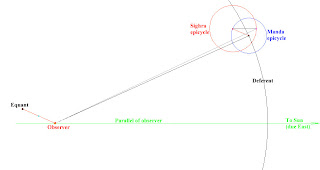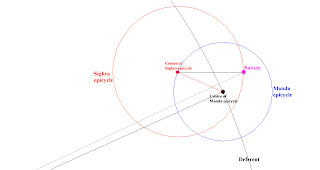
This diagram is by courtesy of Jean-Pierre Lacroix and Robert Baywater, www.ancientcartography.net
In the above diagram, Saturn, a superior planet, is on the circumference of the Sheegra Epicycle, where it is met by a radius drawn parallel to the direction of the Sun from the observer.
To the Western scholars, Indian Astronomy is mysterious. Let us see what astro scholars have said about IA.
Dennis Duke, of Florida State University suggests that Indian Astronomy predates Greek Astronomy
“The planetary models of ancient Indian mathematical astronomy are described in several texts.1 These texts invariably give algorithms for computing mean and true longitudes of the planets, but are completely devoid of any material that would inform us of the origin of the models. One way to approach the problem is to compare the predictions of the Indian models with the predictions from other models that do have, at least in part, a known historical background. Since the Indian models compute true longitudes by adding corrections to mean longitudes, the obvious choices for these latter models are those from the Greco-Roman world. In order to investigate if there is any connection between Greek and Indian models, we should therefore focus on the oldest Indian texts that contain fully described, and therefore securely computable, models. We shall see that the mathematical basis of the Indian models is the equant model found in the Almagest, and furthermore, that analysis of the level of development of Indian astronomy contemporary to their planetary schemes strongly suggests, but does not rigorously prove, that the planetary bisected equant model is pre-Ptolemaic” says he.
The earliest Indian Planetary Models are two sets from the writer Aryabhata, both dating from 6th Century AD.
1) The Sunrise System , after the Epoch, which is taken from the sunrise of 18th Feb 3102 ( Arya Paksha ). It appears first in Aryabhatiya
2) The Midnight System, after the Epoch, which is taken from the midnight of 17/18 FEB 3102 ( Ardha Ratri Paksha ). It appears first in Latadeva’s Soorya Siddhanta
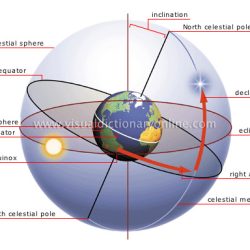
The Local Meridien is taken as Lanka, Longitude 76 degrees, Latitude 0 degrees.