Month: July 2011

In the Concentric Equant Model, reduction to the Heliocentric was easy.

In the above diagram, OM was the Radius of the Epicycle. And q is the Equation of the Center.

The word Equation in Astronomy is the angle between mean planet and true planet. It is got by the formula

q = arcsine ( e* sin (M) )

In the above diagram, BOM is the mean Centrum or the Mean Anomaly and SOM is the true Centrum or the True Anomaly.

t – m = q, the Equation of Center.

This diagram is by courtesy of Jean-Pierre Lacroix and Robert Baywater, www.ancientcartography.net

In the Concentric Equant Model, reduction to the Heliocentric was easy.

In the above diagram, OM was the Radius of the Epicycle. And q is the Equation of the Center.

The word Equation in Astronomy is the angle between mean planet and true planet. It is got by the formula

q = arcsine ( e* sin (M) )

In the above diagram, BOM is the mean Centrum or the Mean Anomaly and SOM is the true Centrum or the True Anomaly.

t – m = q, the Equation of Center.

This diagram is by courtesy of Jean-Pierre Lacroix and Robert Baywater, www.ancientcartography.net

In the Concentric Equant Model, reduction to the Heliocentric was easy.

In the above diagram, OM was the Radius of the Epicycle. And q is the Equation of the Center.

The word Equation in Astronomy is the angle between mean planet and true planet. It is got by the formula

q = arcsine ( e* sin (M) )

In the above diagram, BOM is the mean Centrum or the Mean Anomaly and SOM is the true Centrum or the True Anomaly.

t – m = q, the Equation of Center.

This diagram is by courtesy of Jean-Pierre Lacroix and Robert Baywater, www.ancientcartography.net

w was an important angle in the Munjala Model and the solution to the problem of a difference of 2.5 degrees in the lunar longitude had to be solved. So Munjala brought in an angle, w, angle between the Mean Sun and the Moon’s Apogee.

The angle n is the elongation of the Sun from the Mean Moon and so the

Manda Anomaly, Alpha = w + n

This diagram is by courtesy of Jean-Pierre Lacroix and Robert Baywater, www.ancientcartography.net

w was an important angle in the Munjala Model and the solution to the problem of a difference of 2.5 degrees in the lunar longitude had to be solved. So Munjala brought in an angle, w, angle between the Mean Sun and the Moon’s Apogee.

The angle n is the elongation of the Sun from the Mean Moon and so the

Manda Anomaly, Alpha = w + n

This diagram is by courtesy of Jean-Pierre Lacroix and Robert Baywater, www.ancientcartography.net

w was an important angle in the Munjala Model and the solution to the problem of a difference of 2.5 degrees in the lunar longitude had to be solved. So Munjala brought in an angle, w, angle between the Mean Sun and the Moon’s Apogee.

The angle n is the elongation of the Sun from the Mean Moon and so the

Manda Anomaly, Alpha = w + n

This diagram is by courtesy of Jean-Pierre Lacroix and Robert Baywater, www.ancientcartography.net

The Model propounded by Aryabhata is an algorithm. The Khmers drew the diagrams of the Sun by using the epicyle equivalent of the model developed by Bhaskara in the seventh century. Eccentricity is variable in this Epicycle Model.

You can see a relevant animation of Dennis Duke at
http://people.scs.fsu.edu/~dduke/pingree2.html

The Model propounded by Aryabhata is an algorithm. The Khmers drew the diagrams of the Sun by using the epicyle equivalent of the model developed by Bhaskara in the seventh century. Eccentricity is variable in this Epicycle Model.

You can see a relevant animation of Dennis Duke at
http://people.scs.fsu.edu/~dduke/pingree2.html

The Model propounded by Aryabhata is an algorithm. The Khmers drew the diagrams of the Sun by using the epicyle equivalent of the model developed by Bhaskara in the seventh century. Eccentricity is variable in this Epicycle Model.

You can see a relevant animation of Dennis Duke at
http://people.scs.fsu.edu/~dduke/pingree2.html

The Indian astronomers could calculate the Manda Kendra ( The Equation of Center of Western Astronomy ) and the Manda Phala, but a problem presented itself when calculating the lunar longitude.

The Concentric Model and the Epicylic Model could not calculate Moon’s longitude at quadrature, even though they could calculate the lunar longitude at the times of New Moon and Full Moon. There was a difference of 2.5 degrees between the longitude computed by the Concentric Equant and Epicyclic Models. So the ancients had to give a correction to the Equation of Center, which reached a maximum of 2.5 degrees.

So the Indian astronomers came out with a solution. They created a new Equant (E’), the true Equant, which moves on an epicycle, whose center is the Mean Equant, E. The epicycle has a radius e, equal to EoE., on the Line of Apsis, OA.

q1 = Equation of Center, first lunar inequality
q2 = Correction, second lunar inequality.

True Longitude = Mean long + Eq of Center + q2

The first lunar anomaly was the Evection and the second, the Variation. The first inequality was the Equation of Center and the Evection and the Variation became the second and third inequalities. Actually Indian Astronomy recognised 14 major perturbations of the Moon and 14 corrections are therefore given to get the Cultured Longitude of the Moon, the Samskrutha Chandra Madhyamam. Then Reduction to Ecliptic is done to get the true longitude of Luna !

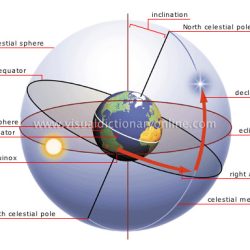
This diagram is by courtesy of Jean-Pierre Lacroix and Robert Baywater, www.ancientcartography.net